Reference Deconvolution Methods
All experiments are imperfect, but in NMR the great majority of instrumental imperfections affect all signals equally. This means that if a signal (e.g. of a reference material such as TMS) can be identified for which the theoretical form is known, the discrepancies between theory and experiment can be used to calculate a correction which restores not just the reference signal, but all the signals in the spectrum, to their correct form.
This turns out to be surprisingly simple; the FIDDLE algorithm (Free Induction Decay Deconvolution for Lineshape Enhancement) developed at Manchester has proved highly successful. Improvements in performance of an order of magnitude have been achieved in experiments such as NOE difference spectroscopy (widely used for structure elucidation) and chiral purity assays (vital in the pharmaceutical industry).
One of the most impressive applications is the suppression of t1-noise in 2D NMR; this can achieve signal-to-t1-noise ratios of over 100000:1, two orders of magnitude better than obtainable by conventional methods.
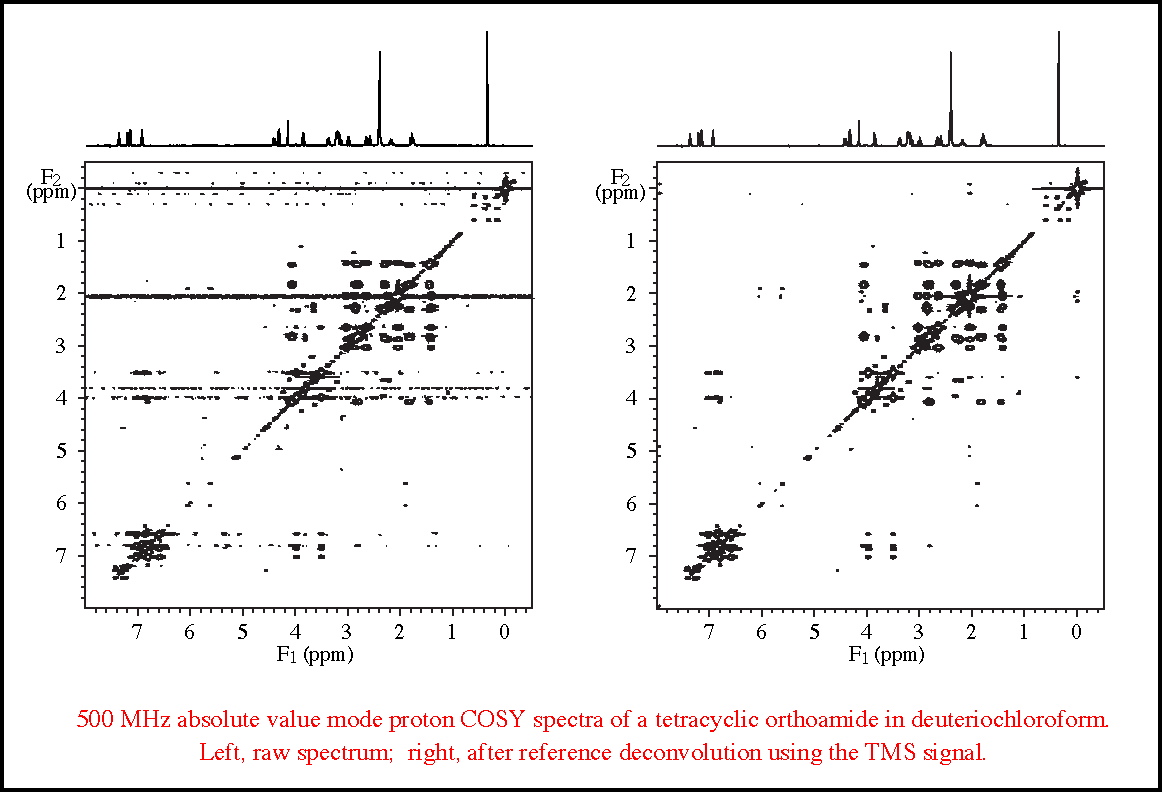
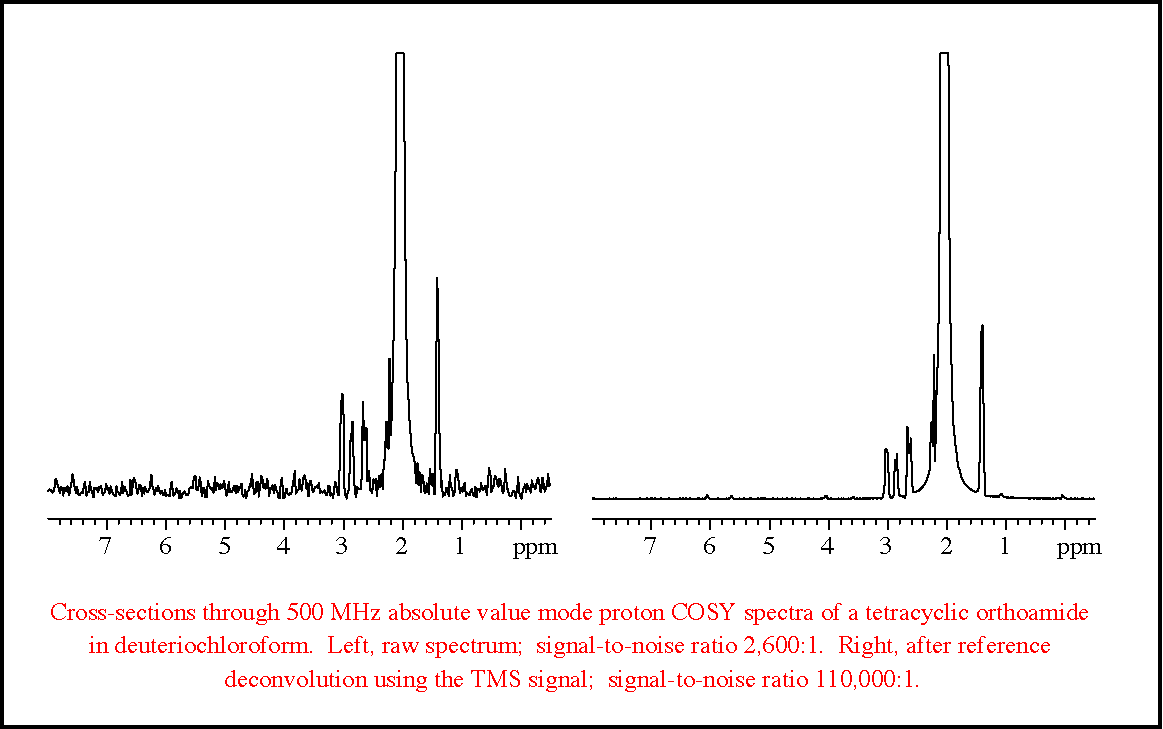
Gibbs, A, Morris GA, Swanson AG, Cowburn D. 1993. Suppression of t1-noise in 2D NMR Spectroscopy by Reference Deconvolution. Journal of Magnetic Resonance Series A. 101:351-356.
Barjat, H, Morris GA, Swanson AG, Smart S, Williams SCR. 1995. Reference Deconvolution Using Multiplet Reference Signals. Journal of Magnetic Resonance Series A. 116:206-214.
Horne, TJ, Morris GA. 1996. Combined Use of Gradient-Enhanced Techniques and Reference Deconvolution for Ultralow t1 Noise in 2D NMR Spectroscopy. Journal of Magnetic Resonance Series A. 123:246-252.
Morris, GA, Barjat H, Horne TJ. 1997. Reference Deconvolution Methods. Progress in Nuclear Magnetic Resonance Spectroscopy. 31:197-257.
Werbelow, LG, Morris GA, Kumar P, Kowalewski J. 1999. Cross Correlated Quadrupolar Spin Relaxation and Carbon-13 Lineshapes in the 13CD2 Spin Grouping. Journal of Magnetic Resonance. 140:1-8.
Morris, GA. 2007 Reference Deconvolution. Encyclopedia of Magnetic Resonance, ed. D.M. Grant and R.K. Harris, J. Wiley and Sons, 9:125-131.
